Einführung
In einer Molkerei werden verschiedene Produkte abgefüllt und hergestellt. Beispielsweise auch Joghurts zu je 150 Gramm. Dabei kommt es bei der Abfüllung zu Schwankungen. Diese Schwankungen werden durch die Standardabweichung bzw. die Varianz erfasst. Je größer die Standardabweichung ist, desto mehr können die Werte der Zufallsgröße X vom Erwartungswert abweichen.
Im Fall der Molkerei ist eine Abweichung von den gewünschten 150g um 5 Gramm noch in Ordnung. Wie wahrscheinlich ist es nun, dass ein Joghurt in Ordnung ist bzw. zu stark von den 150g abweicht?
Eigentlich erstaunlich ist die Tatsache, dass sich eine Wahrscheinlichkeit angeben lässt ohne das eine Wahrscheinlichkeitsverteilung gegeben ist. Aber dies ist auch nicht nötig. In der folgenden Herleitung wird dies deutlich.
Herleitung der allgemeinen Form der Tschebyscheff-Ungleichung
Gesucht ist also die Wahrscheinlichkeit, dass das Gewicht X eines Joghurt zu gering bzw. zu groß ist und damit zu stark vom gewünschten Wert (Erwartungswert E(X) ) abweicht. Ich setze dabei voraus, dass in diesem Beispiel nur auf Gramm genau gemessen werden kann. Man könnte genauso eine genauere (und damit stetige Verteilung) voraussetzen und würde zum gleichen Ergebnis kommen.
So jetzt aber los: Becher im grünen Bereich sind also okay, Becher im roten Bereich weichen zu stark vom gelben Erwartungswert ab.
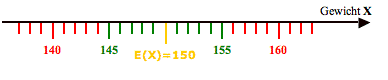
In unserem Fall muss also das Gewicht eines Bechers X im Bereich von 0 bis 144 oder echt über 155 liegen:
X <145 oder X > 155
Oder anders ausgedrückt: Die Abweichung vom gewünschten Gewicht E(X) muss mindestens 6 Gramm betragen:
X-150 ≥ 6
Da ein zu geringes Gewicht eine negative Abweichung bringt (z.B. 127g-150g=-23g), muss nun noch der Betrag genommen werden:
|X-150| ≥ 6
Gesucht ist die Wahrscheinlichkeit hierfür: P(|X-150| ≥ 6) = ?
Da keine Wahrscheinlichkeitsverteilung gegeben ist, kann man den Wert nun nicht mehr exakt ausrechnen. Aber er lässt sich abschätzen. Dazu wird zunächst die Varianz von X betrachtet:
![]()
Jetzt sortiere ich so um, dass alle Terme, die zum roten Bereich gehören beieinander stehen und alle Terme, die sich auf den grünen Bereich beziehen auch nebeneinander:
![]()
Da mich die Terme, die sich auf den grünen Bereich beziehen nicht interessieren, ich möchte ja die Wahrscheinlichkeit im roten Bereich, lasse ich sie einfach weg. Dadurch wird allerdings die Summe auf der rechten Seiten kleiner (oder bleibt gleich, denn die weggelassenen Terme könnten theoretisch ja auch 0 sein):
![]()
Gesucht war die Wahrscheinlichkeit für |X-150| ≥ 6. Um nicht mit Beträgen rechnen zu müssen, kann man links und rechts jeweils das Quadrat nehmen (das geht auf Grund der strengen Monotonie der Betrags- und Quadratfunktion): (X-150)2 ≥ 62. Dabei ist 150 der Erwartungswert E und 6 das Toleranzmaß c. Ich kann damit die Varianz weiter vereinfachen, denn alle Terme (xi-E)2 sind mindestens c2 groß, also eher größer: (xi-E)2 ≥ c2 für alle i.
Durch Ersetzen aller Terme (xi-E)2 durch c2 wird die rechte Seite nochmals abgeschätzt und zusammen mit Ausklammern der c2-Terme erhält man:
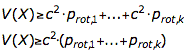
Die Summe der Wahrscheinlichkeiten auf der rechten Seite sind genau die Wahrscheinlichkeiten, die interessieren. Durch Auflösen erhält man also die gewünschte Ungleichung.
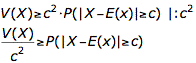
Die Tschebyscheff-Ungleichung 1
Die Wahrscheinlichkeit P, dass eine Zufallsvariable X von dem Erwartungswert E(X) um mehr als das Toleranzmaß c abweicht ist Var(x)/c2 oder mit Var(x)=σ2:
Wahrscheinlichkeit für außerhalb von [E(x)-c;E(x)+c]![]()
oder
Wahrscheinlichkeit für innerhalb von [E(x)-c;E(x)+c]![]()
Diese Ungleichung gilt unabhängig von der zur Grunde liegenden Wahrscheinlichkeitsverteilung, so lange Erwartungswert und Varianz oder Standardabweichung bekannt ist.
Setzt man c=r ⋅ σ, so vereinfacht sich die Ungleichung zu:
![]()
Zu beachten ist noch, dass Abschätzungen nur dann sinnvoll werden, wenn das Toleranzmaß größer als σ ist. Denn sonst erhält man auf der rechten Seiten Werte für Wahrscheinlichkeiten, die nicht zwischen 0 und 1 liegen!
Beispiel 1
Aufgabe
Gegeben ist folgende Notenverteilung einer Schulaufgabe:

a) Berechne Erwartungswert, Varianz und Standardabweichung
b) Mit welcher Wahrscheinlichkeit liegt der Notenschnitt im Bereich [E(X)-2;E(X)+2]? Berechne einmal mit der Tschebyscheff-Ungleichung und einmal exakt!
Lösung
a)
Der Erwartungswert berechnet sich zu
![]()
Als Varianz ergibt sich somit
![]()
Die Standardabweichung beträgt somit ungefähr σ=1,19 .
b) Exakt ergibt sich
![]()
Mit der Tschebyscheff-Ungleichung ergibt sich:
![]()
Deutlich kann man erkennen, wie ungenau die Tschebyscheff-Ungleichung ist. Aber immer noch besser eine schlechte Abschätzung zu haben als gar keine. Und die Bedeutung der Ungleichung liegt auch weniger auf ihrem praktischem Nutzen, sondern eher als Teil von mathematischen Beweisen.
Zum Abschätzen der gewünschten Wahrscheinlichkeit wird also wenigstens die Standardabweichung benötigt. Leider ist die auch nicht bekannt, da hierfür wiederum die Wahrscheinlichkeitverteilung benötigt wird. Wie dieser Wert dennoch ermittelt werden kann, soll hier einmal verdeutlicht werden.
Die Tschebyscheff-Ungleichung für den Mittelwert
Es wird nun einen Stichprobe von der Joghurtproduktion gemacht. Dazu werden n=10 Becher gewogen und festgestellt, ob sie im Toleranzbereich 145 bis 155 Gramm liegen oder nicht.
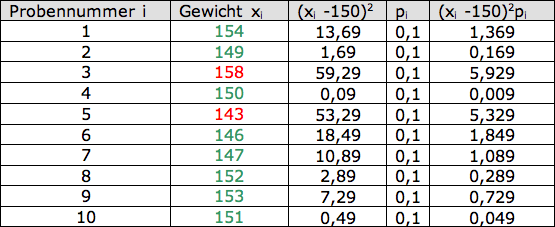
Der Erwartungswert ergibt sich zu 150,3. Die Varianz ergibt sich aus der Summe der letzten Spalte zu Var(X)=16,81. Die Standardabweichung beträgt somit σ=4,1. Damit liegen ca. 68% aller Gewichte im 1σ-Intervall [150,3-4,1 ; 150,3+4,1] = [146,2 ; 154,4] . Stark vereinfacht kann man sagen, dass zwei Drittel aller Joghurtbecher in Ordnung gehen. Noch nicht wirklich gut.
Was einen vielleicht wundert, ist die Tatsache, dass der Erwartungswert gar nicht den 150g entspricht, welche die Joghurts haben sollten. Aber das liegt einfach an dem geringen Stichprobenumfang von nur zehn Bechern. Nehmen wir einfach 100 Becher:
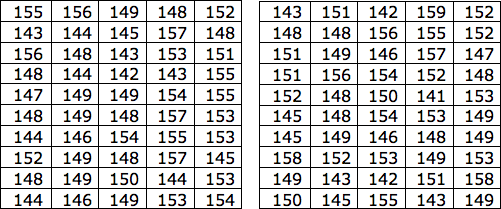
Der Mittelwert ergibt sich nun tatsächlich zu 150 und die Teschebyscheff-Ungleichung lautet
![]() .
.
Für die rechte Seite wird folgender Zusammenhang benutzt:
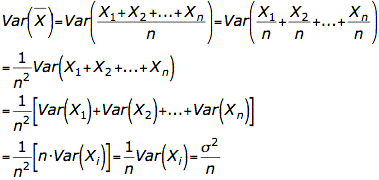
Die Zerlegung in eine Summe von Einzelvarianzen ist erlaubt, da das Befüllen eine Bechers als unabhängig vom vorherigen Becher ist und insgesamt paarweise Unabhängigkeit vorliegt. Diese Einzelvarianzen sind vom Wert alle gleich, da ja n-mal das gleiche Experiment gemacht wurde.
![]()
Nach unendliche viele Befüllung, also für n gegen Unendlich, wird die rechte Seite 0. Bei sehr vielen Befüllungen ist die Wahrscheinlichkeit außerhalb des Toleranzbereichs zu landen also Null. Die durchschnittliche Einfüllmenge nähert sich beliebig genau dem zu erwartenden Wert von 150 an.
Herleitung der Tschebyscheff-Ungleichung 2
Betrachten wir nun noch den ganzen Ablauf als Bernoulliexperiment (Becher korrekt befüllt, nicht korrekt befüllt)
Die Wahrscheinlichkeit eines korrekt befüllten Becher sei p. Der Erwartungswert ist E(X)=np sowie Var(X)=np(1-p).
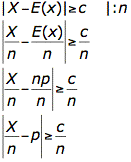
In der Tschebyscheff-Ungleichung ändert sich damit nur der Term auf der linken Seite, da das Teilen durch n eine Äquivalenzumformung war.
![]()
Die rechte Seite der Tschebyscheff-Ungleichung kann wie folgt umgeformt werden:
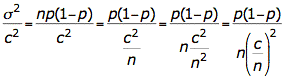
Ersetzt man c:n durch ε ergibt sich die endgültige Form
![]() .
.
Den Term ![]() nennt man auch
Tschebyscheff-Risiko.
nennt man auch
Tschebyscheff-Risiko.
Die rechte Seite lässt sich sogar noch stärker abschätzen. Da p(1-p) vom Funktionsterm eine nach unten geöffnete Parabel mit Scheitel bei (0,5|0,25) ist, sind alle Funktionswerte von p(1-p) maximal 0,25 groß bzw.
![]()
Zusammengefasst ergibt sich
![]()
Mit Hilfe dieser Formeln lässt sich auch das Gesetz der großen Zahlen beweisen. Denn für n gegen Unendlich wird die rechte Seite der Ungleichung Null. Die Wahrscheinlichkeit für einen Unterschied zwischen relativer Häufigkeit und Wahrscheinlichkeit ist für große n Null.
Für die Wahrscheinlichkeit innerhalb des Toleranzintervalls zu liegen folgt
![]()
Es lässt sich somit definieren
Die Tschebyscheff-Ungleichung 2
Liegt einem n-fachem Experiment eine Binomialverteilung mit k Treffern, p als Treffer-Wahrscheinlichkeit und ε>0 zu Grunde, so gilt für die Wahrscheinlickeit innerhalb des Toleranzintervalls zu liegen mindestens bei
![]()
Diese sehr grobe Abschätzung sollte man nur benutzen, wenn in der Aufgabenstellung kein p gegeben ist. Zu dem muss man aufpassen, dass man eine Aussage über die Annäherung der relativen Häufigkeit an die eigentlich Wahrscheinlichkeit macht. Möchte man aber ein Intervall für die Anzahl der Treffer angeben, so muss am Ende der Rechnung das Ergebnis mit n multipliziert werden (ε⋅n=c).
Beispiel 2
Aufgabe
Nach wie vielen Schüssen eines Biathleten kann die Trefferwahrscheinlichkeit des Sportlers mit einer Sicherheit von 80% auf 1% genau angegeben werden?
Lösung
Gegeben ist hier die rechte Seite der Ungleichung mit 80% sowie das Tschebyscheff-Riskiko rT=1%. Die Trefferwahrscheinlichkeit ist nicht gegeben, sondern soll ja statt dessen bestimmt werden. Daher nimmt man obige Formel:
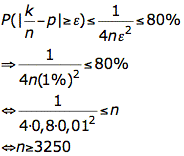
Der Schütze muss also mindestens 3250 schießen, damit man mit achtzigprozentiger Wahrscheinlichkeit eine Aussage über seine Treffsicherheit machen kann.
Die Tschebyscheff-Ungleichung 3
Bei einer Binomial-Verteilung lässt sich die Wahrscheinlichkeit dafür, dass die Stichprobenwahrscheinlichkeit X:n bzw. relative Häufigkeit k:n von der theoretischen Wahrscheinlichkeit p um c:n=ε abweicht, wie folgt abschätzen:
![]()
Beispiel 3
Aufgabe
In einer Urne sind 150 weiße und 50 rote Kugeln. Man zieht 100 mal mit Zurücklegen. In welchem Intervall liegen mit einer Wahrscheinlichkeit von mindestens 90% die Anzahl der weißen Kugeln?
Lösung
Gegeben sind hier n=100 und p=150:200=0,75. Gesucht ist das Toleranzintervall und damit dessen Maßzahl c. Da hier eine Bernoullikette mit bekanntem p vorliegt, wählt man die dritte Gleichung. Die Wahrscheinlichkeit innerhalb des Intervalls zu bleiben, lautet:
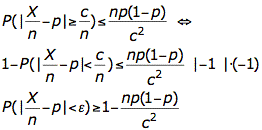
Die rechte Seite soll mindestens 90% sein. Daher folgt mit dem Einsetzen der Werte
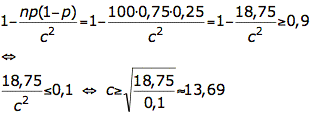
Da der Erwartungswert E(X)=np=75 ist, ergibt sich das Intervall zu [62;88].
Aufgabentypen
