Vorwissen
Bevor es richtig losgeht noch eine kurze Erinnernung an ein paar wichtige Punkte.
- Es kann nicht mit Punkten sondern nur mit deren Ortsvektoren gerechnet werden.
- Ortsvektoren sind die Pfeile, die vom Ursprung bis zum jeweiligen Punkt gehen.
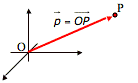
- Ein Punkt und sein Ortsvektor haben die gleichen Koordinaten.
P(2|0|4) und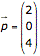
Der Orstvektor hat den gleichen Namen wie sein Zielpunkt nur klein geschrieben. - Der Vektor vom Punkt A nach B wird durch
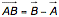 berechnet.
berechnet. - Zwei Vektoren heißen linear abhängig, wenn es eine reelle Zahl k gibt, so dass gilt:
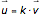
- Parametergleichung:
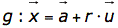
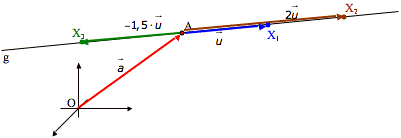
- Das Skalarprodukt zweier Vektoren berechnet sich wie folgt:
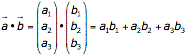
Dabei hat das Skalarprodukt den Wert 0, wenn die Vektoren senkrecht aufeinander stehen. - Der Betrag (Länge) eines Vektors ist
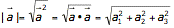
Ebenengleichungen
Paramterform
Eine Ebene ist eine flächige, d.h. zweidimensionale Ansammlung von unendlich vielen Punkten, also eine Menge.
Um alle Punkte einer Ebene erreichen zu können benötigt es daher fünf Dinge:
- Einen Aufpunkt A von dem aus man alle anderen Punkte erreicht werden kann.
- Einen Spannvektor
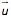 zusammen mit einem reellwertigen Parameter r, der sagt, wie weit man in die eine Richtung zu laufen hat (|r|) und ob vorwärts (r>0) oder rückwärts (r<0).
zusammen mit einem reellwertigen Parameter r, der sagt, wie weit man in die eine Richtung zu laufen hat (|r|) und ob vorwärts (r>0) oder rückwärts (r<0).
- Einen Spannvektor
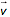 zusammen mit einem reellwertigen Parameter s, der sagt, wie weit man in die eine Richtung zu laufen hat (|s|) und ob vorwärts (s>0) oder rückwärts (s<0).
zusammen mit einem reellwertigen Parameter s, der sagt, wie weit man in die eine Richtung zu laufen hat (|s|) und ob vorwärts (s>0) oder rückwärts (s<0).
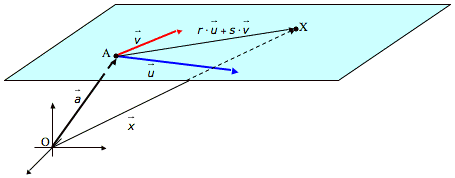 Parametergleichung:
Parametergleichung: 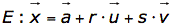
Der Aufpunkt wird durch den Stützvektor festgelegt.
Paramterform
Eine Ebene ist eine flächige, d.h. zweidimensionale Ansammlung von unendlich vielen Punkten, also eine Menge. Um alle Punkte einer Ebene erreichen zu können benötigt es daher fünf Dinge:
- Einen Aufpunkt A von dem aus man alle anderen Punkte erreicht werden kann.
- Einen Spannvektor
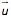 zusammen mit einem reellwertigen Parameter r, der sagt, wie weit man in die eine Richtung zu laufen hat (|r|) und ob vorwärts (r>0) oder rückwärts (r<0).
zusammen mit einem reellwertigen Parameter r, der sagt, wie weit man in die eine Richtung zu laufen hat (|r|) und ob vorwärts (r>0) oder rückwärts (r<0). - Einen Spannvektor
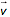 zusammen mit einem reellwertigen Parameter s, der sagt, wie weit man in die eine Richtung zu laufen hat (|s|) und ob vorwärts (s>0) oder rückwärts (s<0).
zusammen mit einem reellwertigen Parameter s, der sagt, wie weit man in die eine Richtung zu laufen hat (|s|) und ob vorwärts (s>0) oder rückwärts (s<0).
 Parametergleichung:
Parametergleichung: ![]()
Der Aufpunkt wird durch den Stützvektor festgelegt.
Diese Schreibweise ist sehr naheliegend, da sie auch im Alltag gerne benutzt wird, wenn man nach dem Weg in einem Hochhaus fragt: "Fahren sie in den zweiten Stock (Stützvektor), dann denn Gang nach rechts (1. Richtungsvektor) und am Ende des Gangs einfach nach links rein (2. Richtungsvektor)."
Auch hier ist es egal, welchen Punkt der Ebene man als Stützpunkt verwendet.
Ebenso ist es unerheblich, ob bestimmte Vektoren als Richtungsvektoren gewählt werden, solange die neuen Richtungsvektoren von den alten Richtungsvektor linear abhängen, also ebenfalls in der Ebene liegen.
Es gibt aber nicht nur diese Schreibweise. Wenn man sich genauer überlegt, wie man eine Ebene im Raum eindeutig festlegen kann, so kommt man schnell auf 2 Punkte.
- Man muss angeben, wie die Ebene im Raum liegt. "Wie schief" sie ist (Normalenvektor)
- Und um wie viel sie vom Ursprung entfernt ist, also den Aufpunkt.
Mit Hilfe dieser zwei Komponenten lässt sich eine Ebene nun in der sogenannten Punkt-Normalenform angeben.
Punkt-Normalenform
Ein Normalenvektor steht immmer senkrecht auf dem Vektor ![]() vom Aufpunkt P zu allen Punkten der Ebene X. Daher muss das Skalarprodukt immer den Wert Null haben.
vom Aufpunkt P zu allen Punkten der Ebene X. Daher muss das Skalarprodukt immer den Wert Null haben.
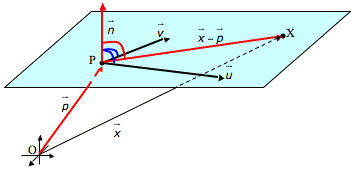 Punkt-Normalenform:
Punkt-Normalenform: ![]()
Normiert man den Normalenvektor auf die Länge 1 (![]() ), so erhält man die Hessesche Normalenform
), so erhält man die Hessesche Normalenform ![]() .
.
Wenn gleich diese Ebene-Gleichung auch sehr eingängig sein mag, so sind diese beiden ersten Ebenengleichung eigentlich sehr ungewohnt.
Man ist doch eher an Geradengleichung gewohnt ![]() ,
die einen Zusammenhang zwischen den Koordinaten x und y herstellt.
,
die einen Zusammenhang zwischen den Koordinaten x und y herstellt.
Das Gleiche lässt sich auf Ebenen übertragen. Parameterformen und Punkt-Normalenformen lassen sich jeweils in die Koordinanteform umrechnen. Das dabei die Anschaulichkeit verloren geht, nimmt man gerne in Kauf, da sich die ein oder andere Rechnung stark vereinfachen wird.
Koordinatenform
Die Koordinatenform einer Ebene lautet:
![]()
oder mit den bekannten Variablen x, y, z
![]()
Die Paramter a,b,c,d sind reelle Zahlen.
Grundaufgaben
Gegeben sind die 3 Punkte A,B und C. Stelle eine Ebenengleichung in Parameterform auf!
- Wähle einen Punkt als Stützpunkt, z.B. A.
- Berechne
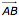 .
.
- Berechne
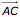 .
.
- Prüfe,
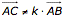 , also die lineare Unabhängigkeit der Spannvektoren.
, also die lineare Unabhängigkeit der Spannvektoren.
Gegeben ist eine Ebene E in Parameterform 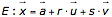 .
.
Gib die entsprechende Normalenform 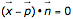 an!
an!
Der Normalenvektor der Ebene ist das Kreuzprodukt der Spannvektoren 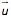 und
und 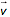 :
:
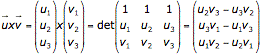
Einfacher zu merken in der folgenden Merkregel:
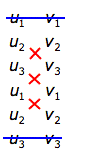
- Als Punkt kann man einfach den Stützpunkt der Ebene nehmen.
Gegeben ist eine Ebene E in Normalenform 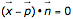 .
.
Gib die entsprechende Koordinatenform 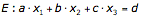 an!
an!
Die Koordinaten des Normalenvektors entsprechen den Parametern in der Koordinantengleichung. Man erhält somit bereits
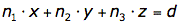
Den Parameter d erhält man, in dem man eine Punkt in die vorhandene Gleichung einsetzt und d berechnet. Man wählt hier den Punkt P.
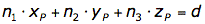
Gegeben ist eine Ebene E 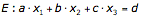 in Koordinatenform.
in Koordinatenform.
Gib die entsprechende Parameterform 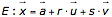 an!
an!
Schreibe für b und c die Variablen r und s und löse nach x auf
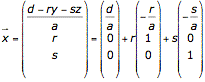
Gegeben ist eine Ebene E in Parameterform. Wo schneidet diese Ebene die Koordinatenachsen?
- Löse nacheinander die linearen Gleichungssysteme:
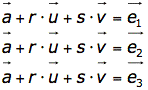
Beispiele
Beispiel 1
Aufgabe
Der Vektor 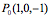 liege auf der Ebene E mit dem Normalenvektor
liege auf der Ebene E mit dem Normalenvektor 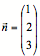 . Stelle die
Koordinatenform der Ebene auf!
. Stelle die
Koordinatenform der Ebene auf!
Lösung
Die Koordinaten des Normalenvektors sind die Paramter in der Koordinatenform.
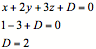
Insgesamt ergibt sich somit  .
.
Rechner
Umrechnungen
in umrechnen.
Links
- Determinanten
Rechner für Determinanten.
- Lösen Lineare Gleichungssysteme
Gegeben sind die 3 Punkte A,B und C. Stelle eine Ebenengleichung in Parameterform auf!
- Wähle einen Punkt als Stützpunkt, z.B. A.
- Berechne
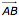 .
. - Berechne
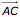 .
. - Prüfe,
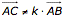 , also die lineare Unabhängigkeit der Spannvektoren.
, also die lineare Unabhängigkeit der Spannvektoren.
Gegeben ist eine Ebene E in Parameterform 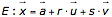 .
.
Gib die entsprechende Normalenform 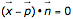 an!
an!
Der Normalenvektor der Ebene ist das Kreuzprodukt der Spannvektoren
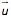 und
und 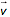 :
: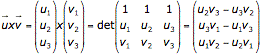
Einfacher zu merken in der folgenden Merkregel:
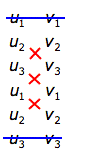
- Als Punkt kann man einfach den Stützpunkt der Ebene nehmen.
Gegeben ist eine Ebene E in Normalenform 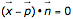 .
.
Gib die entsprechende Koordinatenform 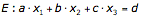 an!
an!
Die Koordinaten des Normalenvektors entsprechen den Parametern in der Koordinantengleichung. Man erhält somit bereits
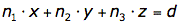
Den Parameter d erhält man, in dem man eine Punkt in die vorhandene Gleichung einsetzt und d berechnet. Man wählt hier den Punkt P.
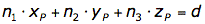
Gegeben ist eine Ebene E 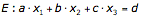 in Koordinatenform.
in Koordinatenform.
Gib die entsprechende Parameterform 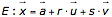 an!
an!
Schreibe für b und c die Variablen r und s und löse nach x auf
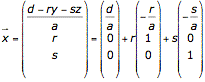
Gegeben ist eine Ebene E in Parameterform. Wo schneidet diese Ebene die Koordinatenachsen?
- Löse nacheinander die linearen Gleichungssysteme:
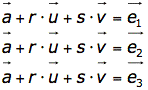
Beispiel 1
Aufgabe
Der Vektor ![]() liege auf der Ebene E mit dem Normalenvektor
liege auf der Ebene E mit dem Normalenvektor ![]() . Stelle die
Koordinatenform der Ebene auf!
. Stelle die
Koordinatenform der Ebene auf!
Lösung
Die Koordinaten des Normalenvektors sind die Paramter in der Koordinatenform.
![]()
Insgesamt ergibt sich somit ![]() .
.
Umrechnungen
in umrechnen.
Links
- Determinanten
Rechner für Determinanten. - Lösen Lineare Gleichungssysteme