Vorwissen
Bevor es richtig losgeht noch eine kurze Erinnernung an ein paar wichtige Punkte.
- Es kann nicht mit Punkten sondern nur mit deren Ortsvektoren gerechnet werden.
- Ortsvektoren sind die Pfeile, die vom Ursprung bis zum jeweiligen Punkt gehen.
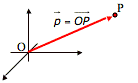
- Ein Punkt und sein Ortsvektor haben die gleichen Koordinaten.
P(2|0|4) und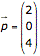
Der Orstvektor hat den gleichen Namen wie sein Zielpunkt nur klein geschrieben. - Der Vektor vom Punkt A nach B wird durch
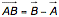 berechnet.
berechnet. - Zwei Vektoren heißen linear abhängig, wenn es eine reelle Zahl k gibt, so dass gilt:
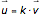
- Parametergleichung:
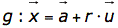
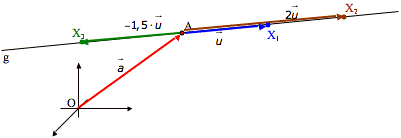
- Das Skalarprodukt zweier Vektoren berechnet sich wie folgt:
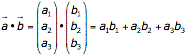
Dabei hat das Skalarprodukt den Wert 0, wenn die Vektoren senkrecht aufeinander stehen. - Der Betrag (Länge) eines Vektors ist
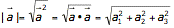
Schnitte Gerade-Ebenen
Gegeben ist eine Ebene E in Parameterform. Wo schneidet diese Ebene die Koordinatenachsen?
- Löse nacheinander die linearen Gleichungssysteme:
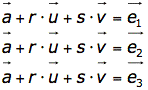
Berechne die Lage der Geraden g zur Ebene E und ggf. den Durchstoßpunkt S!
Berechne die Lage der Geraden ![]() zur Ebene
zur Ebene ![]() und ggf. den Durchstoßpunkt S!
und ggf. den Durchstoßpunkt S!
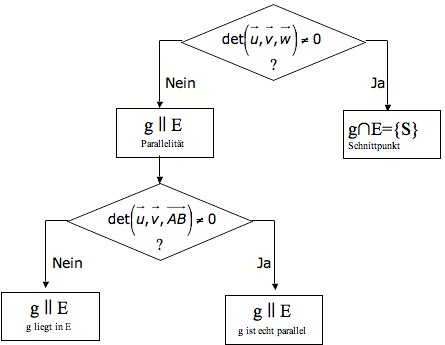
Die Aufgabe vereinfacht sich extrem, wenn die Ebene nicht in Parameterform, sondern in Koordinatenform gegeben ist. Dann lässt sich nämlich aus der Geradengleichung zeilenweise ein Ausdruck für x1,x2,x3 entnehmen und in E einsetzen. Man erhält nur noch eine Gleichung mit einer Unbekannten. Je nach Anzahl der Lösungen hat man dann den Fall "liegt in" (unendlich viele Lösungen), "durchstößt in" (genau eine Lösung) oder "verläuft echt parallel" (keine Lösung).
Beispiele
Überprüfe die Lage der Geraden g und Ebene E
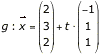 und
und 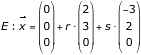
Lösung
1. Schritt
Beim Rechnen ohne Determinanten würde man die beiden gegebenen Gleichungen gleichsetzen und je nach Anzahl der Lösungen entscheiden, welcher Fall vorliegt. Bei unendlich vielen Lösungen ist g in E, bei 1 Lösung schneidet g die Ebene E, bei keiner Lösung verläuft die Gerade g parallel zu E.
Beim Rechnen mit Determinanten beginnt man zunächst genauso:
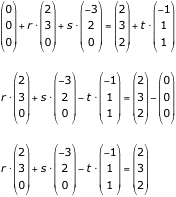
Um die Cramerscher Regel anwenden zu können, wird das Minuszeichen vor t in den Vektor rein gezogen und man erhält:
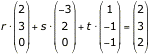
Dieses lineare Gleichungssystem entspricht
![]()
Damit ist zunächst die Determinante ![]() zu bestimmen. Ist diese ungleich Null, so sind die drei Vektoren linear unabhängig.
zu bestimmen. Ist diese ungleich Null, so sind die drei Vektoren linear unabhängig.
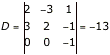
Die Determinante ist ungleich Null, damit scheidet g die Ebene E.
2. Schritt
Nun ist der Schnittpunkt zu bestimmen. Dieser berechnet sich wie folgt (Cramersche Regel):
Da der Vektor ![]() der
Richtungsvektor der Geraden ist (mal (-1)), wird dieser auch in der
Determinante durch
der
Richtungsvektor der Geraden ist (mal (-1)), wird dieser auch in der
Determinante durch 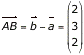 ersetzt werden.
Denn es genügt ja zu wissen, um wie viel man von B (Stützpunkt der Geraden) zu
laufen hat, um den Schnittpunkt zu erreichen.
ersetzt werden.
Denn es genügt ja zu wissen, um wie viel man von B (Stützpunkt der Geraden) zu
laufen hat, um den Schnittpunkt zu erreichen.
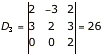 und damit ist
und damit ist
![]() .
.
Setzt man diesen Wert in die Geradengleichung ein, erhält
man den Schnittpunkt: 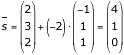 .
Der Durchstoßpunkt hat die Koordinaten S(4|1|0).
.
Der Durchstoßpunkt hat die Koordinaten S(4|1|0).
Schnitte Ebene-Ebene
Berechne die Lage der Ebene E1 zur Ebene E2
Beide Ebenen in Parameterform
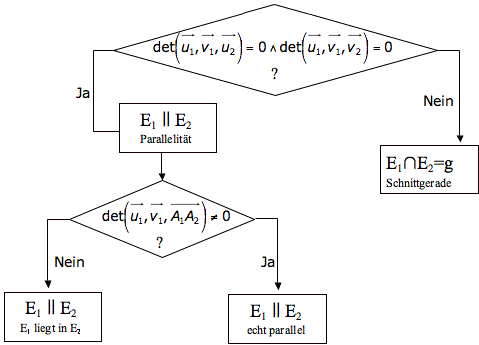
Ebenen in Koordinaten-, Normalenform
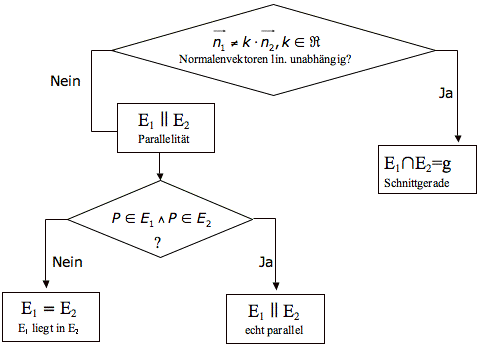
Im Folgenden werden nun Rechner angeboten, die die Kontrolle von Hausaufgaben ermöglichen oder bei der Erstellung von Schulaufgaben helfen sollen.
Rechner
Schnitt von einer Geraden mit einer Ebene 1
Einzugeben sind ![]() und
und ![]()
Schnitt von einer Geraden mit einer Ebene 2
Einzugeben sind ![]() und
und ![]() . Eventuell muss die Normalform erst in Koordinatenform umgewandelt werden.
. Eventuell muss die Normalform erst in Koordinatenform umgewandelt werden.
Schnitt zweier Ebenen 1
Einzugeben sind ![]() und
und ![]()
Schnitt zweier Ebenen 2
Einzugeben sind ![]() und
und ![]() . Gegbenenfalls muss die Normalform erst in Koordinatenform umgewandelt werden.
. Gegbenenfalls muss die Normalform erst in Koordinatenform umgewandelt werden.
Schnitt zweier Ebenen 3
Einzugeben sind 2 Ebenen in der Form ![]() .
.
Übungsaufgaben
Schnitt einer Geraden mit einer Ebene
Nur ganzzahlige Lösungen| g: |
|
= |
|
+ r · |
|
| E: |
|
= |
|
+ r · |
|
+ s · |
|
Die Lösungen können über den Rechner bestimmt werden.
Links
- Determinanten
Rechner für Determinanten. - Lösen Lineare Gleichungssysteme