Einführung
Ausgehend vom Würfeln möchte ich den Begriff der Zufallsgröße, Wahrscheinlichkeitsfunktion und Dichtefunktion in den wichtigsten Schritten erklären. Hierbei kommt es mir zunächst nicht auf die Vollständigkeit an, dazu ist das Thema zu komplex für den normalen Schulalltag, sondern auf das Verständis der Problematik.
Definition: Zufallsgröße
Die Zufallsgröße oder Zufallsvariable ist eine Funktion, die jedem Ergebnis einen reellen Wert zuordnet:
![]()
Beispiel 1
Im ersten Beispiel interessiert die Augenzahl:
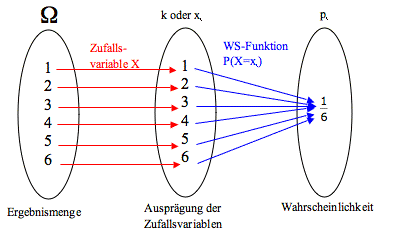
Im folgenden Beispiel interessiert nur, ob eine Sechs gewürfelt wird oder nicht.
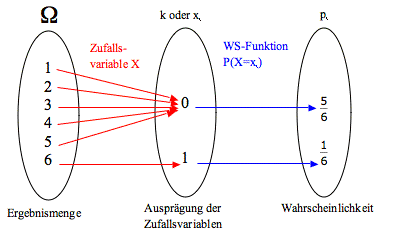
Beide Fälle sind typische Beispiele, wie sie in vielen Büchern zu finden sind. Andere Beispiele wären Kartenspiele, Roulette, Glücksräder etc. Allerdings fragt man sich dann relativ schnell, warum die Zufallsvariable eine Funktion ist, die auf die reelen Zahlen abbildet.
Dies hat zwei Gründe:Zum Einen möchte man die Zufallsgröße als Variable beim Ausrechnen der Wahrscheinlichkeit benutzen und Funktionen sind in der Schule eigenlich immer auf ganz R definiert. Zum Anderen gibt es Situationen, in denen
ein Abbilden auf die natürlichen Zahlen wie oben nicht genügen würde. Man denke an- den Wasserstand X -> Wie hoch ist die Wahrscheinlichkeit für Hochwasser: P(X>9,50m)
- oder Temperaturen Y -> Wie hoch ist die Wahrscheinlichkeit für Frost im April: P(Y<0 Grad)
In beiden Fällen können Kommazahlen oder zusätzlich negative Zahlen auftauchen.
Die Werte aus dem zweiten Fall "nur Sechser" lassen sich auch in ein Koordinatensystem (Histogramm) übertragen. Man erhält:
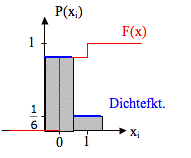
Dabei sollte der Augenmerk besonders auf der blauen Randfunktion (Dichtefunktion), dem darunterliegenden, grauen Flächeninhalt und der roten Verteilungsfunktion F(X) liegen. Die Verteilungsfunktion ist dabei die Summe der Wahrscheinlichkeiten bis k, also P(X≤k).
Definition: Wahrscheinlichkeitsfunktion
Die Wahrscheinlichkeitsfunktion ordnet jedem möglichen Wert der Zufallsgröße einen Wert zu.
Eigenschaften:
- 0≤P(X=xi)≤1
- Die Summe über alle P(X=xi) muss 1 ergeben (Normierung, Komlogorov-Axiome)
Jetzt wird das Zufallsexperiment komplexer. Man würfelt mit 2 Würfeln und betrachtet die Augenzahlpaare (36 Stück). Die blaue Linie stellt wieder die Wahrscheinlichkeitsfunktion P(x) dar. Der Flächeninhalt summiert sich zu 1 auf, wie man an der roten Linie sehen kann. Diese endet beim Funktionswert 1.
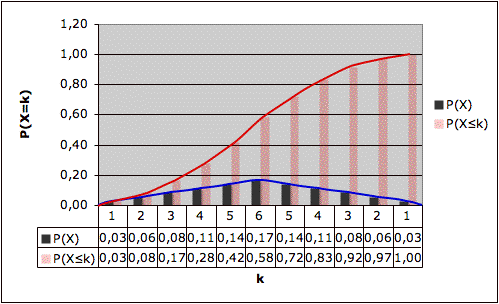
Nun geht man noch ein Stück weiter und geht zu einer Zufallsgröße über deren Werte so fein sind, dass man sie gar nicht mehr wirklich unterscheiden kann (Wasserstand) bzw. bei der eine Unterscheidung keinen Sinn macht. So macht es beispielsweise beim IQ keine Rolle, ob man einen Wert von 110 oder 109,999991 hat. Man interessiert sich eher für P(109,5≤X≤110,5). D.h. man interessiert sich dafür wie sich die Wahrscheinlichkeit auf die Intervalle ]x;x+dx] verteilt.
Definition: Dichtefunktion
Die Dichtefunktion f ordnet jedem der unendlich viele Werte einer Zufallsgröße keinen Wert zu!
Viel mehr gilt, dass im Gegensatz zur Wahrscheinlichkeitsfunktion einer diskreten Zufallsgröße die Dichtefunktion im Punkt X nicht die Wahrscheinlichkeit dafür angibt, dass die Zufallsgröße den Wert X annimmt. Bestimmbar ist nur die Wahrscheinlichkeit, dass der Wert von X innerhalb eines bestimmten Intervalls ]x;x+dx] liegt. Sie entspricht der Fläche unterhalb der Dichtefunktion über diesem Intervall. Es gilt:
![]()
Es kann aber nun nicht geschlossen werden, dass das Ergebnis k unmöglich ist nur weil die Wahrscheinlichkeit aufgrund des unendliche schmalen Streifens unterhalb des Graphens der Dichtefunktion nicht berechnet werden kann. Die Einzelwahrscheinlichkeit ist zwar Null, aber man kann eine Wahrscheinlichkeit für einen Bereich dafür angeben.
Eigenschaften:
- 0≤fi≤1
- Die Summe über alle fi muss 1 ergeben (Normierung, Komlogorov-Axiome). Da hier aber unendlich viele Summanden auftreten und die Streifen
eine Breite von dx haben, benutzt man nun die Integralschreibweise:
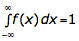
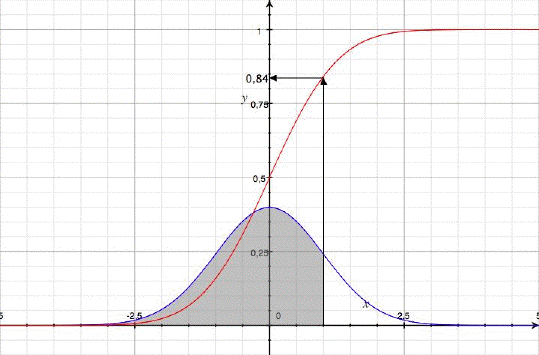
Der rote Graph ist P(x≤k), wobei hier der Wert für k=1 eingezeichnet wurde. Sie entspricht der Verteilungsfunktion F(X)=P(X≤k). Der blaue Graph ist die Dichtefunktion f(X).
Definition: Verteilungsfunktion
Die Verteilungsfunktion ist die Summe (Integral) der Einzelwahrscheinlichkeiten bis k:
![]()
Damit ist die Ableitung der Verteilungsfunktion die Dichtefunktion, wenn die Verteilungsfunktion stetig ist.
Diese etwas merkwürdige Art der Definition ist notwendig, um so die "Wahrscheinlichkeitsintervalle" ausrechnen zu können:
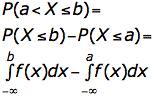
So ließe sich nun ausrechnen, wie wahrscheinlich es ist, einen IQ von 100 mit einer Abweichung von 0,5 Punkten zu haben. Die Einzelwahrscheinlichkeit für exakt 100 ist dagegen (rein mathematisch) Null.
Oftmals genügen aber Wahrscheinlichkeits- bzw. Dichtefunktion nicht aus, um gewünschten Aussagen machen zu können. So ist es bei Glücksspielen für den Betreiber wichtig zu wissen, welchen Gewinn ein Spieler zu erwarten hat. Man spricht daher vom sogenannten Erwartungswert. Dieser entspricht anschaulich dem durchschnittlichen Wert, den ein Spieler bekommt und wird genauso wie der Notendurchschnitt einer Schulaufgabe berechnet.
Definition: Erwartungswert
Für eine diskrete Zufallsgröße gilt:
![]()
Für stetige Zufallsgröße benötigt man die Dichtefunktion :
![]()
Ist im diskreten Fall die Wahrscheinlichkeit für jedes Ergebnis auch noch gleich (Binomialverteilung), so lässt sich der Erwarttungswert über E(X)=np berechnen. Der Erwartungswert für die Augenzahl beim Würfeln ist also (1+2+3+4+5+6)*1/6 = 3,5.
Der Erwartungswert ist die Stelle in obigen Diagrammen mit dem höchsten Wert. Links und rechts vom Erwartungswert liegen mehr oder weniger stark verstreut die restlichen Werte. Genau diese Streuung ist ist interessant, wenn es darum geht, wie weit und häufig sich die Werte verteilen.
Definition: Varianz und Standardabweichung
Die Varianz gibt an, wie stark die Ergebnisse eines Zufallsexperiments sich um den Erwartungswert herum verteilen bzw. abweichen.
Für eine diskrete Zufallsgröße gilt:
![]()
Für stetige Zufallsgröße benötigt man die Dichtefunktion :
![]()
Die Abweichung wird quadratisch genommen, damit diejenigen Werte, die weiter entfernt vom Erwartungswert liegen ein höheres Gewicht bekommen. Möchte man die stärker abweichenden Werte nicht so sehr gewichten, so berechnet man die Standardabweichung:
![]()
Beispiel 2
Aufgabe
In einer Urne liegen 2 rote und 4 blaue Kugeln. Ohne zurücklegen werden die Kugeln gezogen. Wie oft muss man wahrscheinlich ziehen, um beide roten zu haben.
Lösung
Die Zufallsvariable X zählt die Anzahl der gezogenen Kugeln, denn darüber muss man später eine Aussagen machen.
Nun gibt es die Möglichkeit beide roten Kugeln direkt hintereinander zu ziehen bis zu ich muss alle Kugeln gezogen haben. Mit Hilfe eines Baums oder einer Tabelle kommt man auf folgende Wahrscheinlichkeiten:
- P(X=2)=1/15
- P(X=3)=2/15
- P(X=4)=3/15
- P(X=5)=4/15
- P(X=6)=5/15
Der Erwartungswert ist E(X)=2*1/15+3*2/15+4*3/15+5*4/15+6*5/15=4,7 . Man benötigt also wahrscheinlich 5 Züge um beide roten zu erwischen.
Im Vergleich der Begriffe stellt sich alles wie folgt dar:
| Ergebnisse | diskrete Verteilung | kontinuierliche Verteilung | |
| Beispiele | Würfeln, Roulette, ... | Wasserstand, Temperatur, IQ, ... | |
| Wahrscheinlichkeitsverteilung | P(X=k) ∈ [0;1] | - | |
| Dichtefunktion | - | f(k) = P(k<X<k+dx) ∈ [0;1] | |
| Normierung | ∑P(X=k) = 1 | ||
| Verteilungsfunktion | ∑P(X≤k) | ||
| Erwartungswert | |||
| Varianz |